Ever wondered how the surface area of an irregular polygon is calculated?

Perhaps you wanted to determine the area enclosed by specific coordinates on a Google Map or OSM?

We are going to write a python script using Green’s Theorem to calculate the area of an irregular polygon using coordinates of the points.

Green’s theorem is used in area surveying to determine the area and centroid of plane figures by integrating over the perimeter. The area can be computed using this formula:

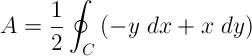
where C is a closed contour or curve that defines the boundary of the region D, and A is the area of the region D.

We will discuss Green’s Theorem in a later article, but for now we are focusing on this specific application of Area.

This is a python script based on the formula above:

1
2
3
4
5
6
7

#!/usr/bin/python -tt
def area(p):
    return 0.5 * abs(sum(x0*y1 - x1*y0
                         for ((x0, y0), (x1, y1)) in segments(p)))

def segments(p):
    return zip(p, p[1:] + [p[0]])

Breaking the code:

1. Obtain the coordinates of the vertices.
2. Create an array of the x and y coordinates of each vertex in a counterclockwise order – Repeat the first pair at the end of the array (list).
3. Multiply the x coordinate of each vertex by the y coordinate of the next vertex, then add the results and call it S1.
4. Multiply the y coordinate of each vertex by the x coordinate of the next vertex, then add the results again and call it S2.
5. Now Subtract S1 from S2 to get 2A = S2 – S1.
6. Now divide the difference by 2 to get the Area (A).

— Citations: How to Calculate the Area of a Polygon: WikiHow Green’s Theorem: Wolfram Python code: Stack Overflow